Axioms for Life

Believe in God. Believe that he is, and that he created all things, both in heaven and in earth. Believe that he has all wisdom, and all power, both in heaven and in earth. Believe that man does not comprehend all things that the Lord can comprehend. And again, believe that ye must repent of your sins, and forsake them, and humble yourselves before God, and ask in sincerity of heart that he would forgive you...

I would like to begin with the Biblical imperative for studying mathematics. Where in the Bible does it say that we should study mathematics? Genesis 1:30 says, "Multiply and replenish the earth." Also, in I Thessalonians 5:21 we read, "Prove all things. Hold fast that which is good." Now I understand that the word "prove" in this context means to "test" all things, but when a mathematician sees the word "prove", it carries a special meaning, and that is the subject of this discussion.

For a mathematician, proving things is a matter of sorting statements into two categories, or boxes, labeled "True" and "False". The sorting is done in such a way that each statement that goes into the "True" box must be accompanied with a demonstration that it should be there. Likewise, each statement that goes into the "False" box must be accompanied with a demonstration that it is false. Mathematicians call the kind of system that allows such a sort an axiomatic system.

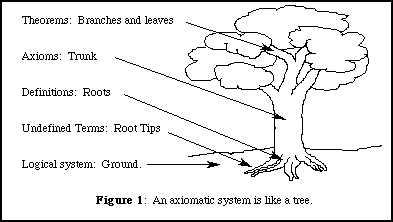
Let us compare an axiomatic system to a tree. (See FIGURE 1) First, there must be a logical system that allows us to make inferences. That is, we must have some way to decide on the truth of statements based on the truth of other statements. The logical system is like the ground in which a tree is planted. While the ground is not actually part of the tree, it is necessary in order for the tree to be planted and to grow.

The next two components of any axiomatic system are the undefined terms and the definitions. Every axiomatic system has basic terms from which its statements are made. These terms are like the roots of the tree. The undefined terms are the starting point for every definition and statement of the system. They are the root tips on the tree. All other terms of the system are built up by combining undefined terms in various ways in statements called definititions. These are the roots of the tree.

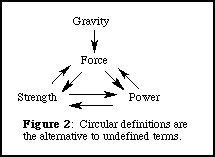
Now it is easy to understand why we must define terms carefully, but it may not be as obvious why we must include undefined terms. Suppose, for example, that we want to define "gravity". If you look up "gravity" in the dictionary, it says something like "gravity is a force that pulls things together." So, in order to understand gravity, we need to know what a force is. If you look up "force", you will find that "force" means "strength or power", so you need to look up these words as well. "Strength" means "to be strong." This is a circular definition, since the words "strength" and "strong" are essentially the same word. We also find that "strength" means "force", another circular reference, or "power". "Power", we are not surprised to learn, means "force", or "strength", precisely the words that we were trying to define in the first place. It is clear that if we try to define everything, that eventually the process must end with circular references. (See FIGURE 2) The alternative is to recognize that the basic terms of any system must be undefined. For example, we could have a system in which "force" is undefined. Then we could define "gravity" as a force, and tell how strong the force is, and on what objects it acts, etc. As another example, in Euclidean geometry we typically take "point" and "line" as undefined terms of the system. This does not mean that we cannot try to define these terms in terms of other constructs, but only that the most basic terms of the system must necessarily be undefined.

The next two components of an axiomatic system are the axioms and theorems. In terms of the tree analogy, the axioms are the base of the tree, and the theorems are the branches growing out of that base. Axioms and theorems are the statements. The axioms are statements that are the base of the system, and the theorems are the statements that can be deduced from the axioms to be true. To illustrate, consider the famous "Pythagorean theorem" of geometry. It says "The square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides." This theorem is a statement about the relationship between the lengths of sides of a right triangle. The fact that it goes into the "True" box depends on the truth of other statements about the relation between the area of a triangle and the area of a rectangle, etc. These statements in turn depend on other statements. The process ends in the axioms, which are the basic statements that we accept as a starting point for the system. There must necessarily be such statements which are not proved in any system, just as there must be undefined terms. The only alternative is to have circular proofs, which are clearly unhelpful in sorting statements.

To summarize, axiomatic systems have five general parts. As a tree must be planted in the ground, so also an axiomatic system must have a logical system of rules for inference in order to exist. The roots at the base of the tree correspond to the undefined terms and the definitions of the system. The trunk of the tree corresponds to the axioms, which are the statements that serve as a starting point for the system. Finally, the branches are the theorems, the statements which grow out of the axioms and clarify what is implicitly true within the axioms.

Having seen what axiomatic systems are, let us turn our attention to basic characteristics of axiomatic systems that are useful to our understanding of the world. First, we observe that any useful axiomatic system must have some statements in the "true" box and some in the "false" box. If the system does not allow us to distinguish between the two, then it is not very useful. This seems so obvious that it hardly needs to be mentioned, but there are a great many axiomatic systems that do not meet this requirement, as we shall see. Our second observation is that some statement about existence should appear in the "true" box. If the axioms cannot be used to show that something exists, then the system is not very helpful to our understanding the world. Finally, it would be very nice if every statement within the axiomatic system could be sorted into either the "true" or the "false" box. While some axiomatic systems can be shown to have this characteristic, some important mathematical systems can be shown to lack this characteristic, and I believe that this fact has far reaching consequences for the understanding of all axiomatic systems.

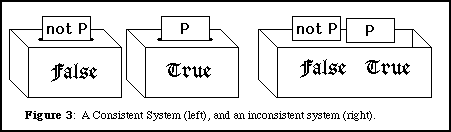
Let us first consider what is required in order to distinguish between statements in the "true" box and those in the "false" box. In our logical system, each statement has a negation. If P represents a statement, then not-P represents its negation. It is fundamental to the sorting process that if P is true, then not-P is false, and vice versa. In other words, if one can prove that P goes into the "true" box, then that same proof shows that not-P goes into the "false" box. Now suppose it were possible to prove that both P and not-P go into the same box. Then there can be only one box. Every statement goes into the same box, and there is no sorting possible! Such a system, in which a statement and its negation are both true is said to be inconsistent. In order for any sorting to be done, the system must be consistent. That is, it must not be possible to prove any statement and its negation.

Our second observation is that in order to have an existence statement as a theorem, it is necessary to have an existence statement as an axiom.. In the next four paragraphs we will attempt to demonstrate our reason for saying this. (If this is already obvious to you, feel free to skip the next four paragraphs.)

At a basic level, the statements that make up an axiomatic system are all about the properties of undefined terms of that system. There are two basic types of statements. Those which assert that particular elements have a given property are called existence statements. Those which assert that all elements of the system have a given property are called categorical statements.

A fundamental property of our logical system is that the negation of an existence statement is always a categorical statement, and vice versa. For example, the statement "every pair of points lies on a line" is categorical. It asserts that lying on a line is a property common to all pairs of points in the system. The negation of this statement is the assertion that some pair of points does not posses this property, that is, "there exists a pair of points that does not lie on a line." This is an existential statement. In any consistent axiomatic system that includes the terms point, line, and on, only one of these two statements belongs in the "true" box. Which one belongs there, of course, depends on the particular set of axioms under consideration.

Now if we can construct (mentally or physically) a model in which all the axioms of a system are verifyably true statements about the model, then all the theorems of the system must necessarily be true of the model as well. It follows that any statement that is false about the model cannot possibly be a theorem of the system.

Now suppose that a consistent axiomatic system does not contain an existence axiom. We claim that it cannot then have an existence theorem. To see this, let us consider a model in which none of the undefined terms of the axiomatic system exists. This model is called the empty model. By definition, every existence statement of the axiomatic system must be a false statement about the empty model. It follows that the negation of each existence statement must be a (vacuously) true statement about the model. In particular, every possible categorical statement of the system is true of the model, and this list contains every axiom of the system! Having established that the empty model is actually a model of our system, we then observe that existence statements (false statements about the model) cannot be theorems of the axiomatic system. In other words, if there is no existence axiom, then there is no existence theorem, as claimed.

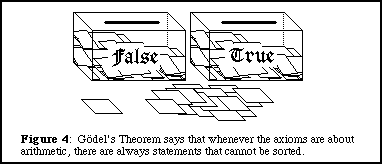
Finally, if it is possible to sort all the possible statements of an axiomatic system into "true" or "false" boxes, then the system is said to be complete. One of the most startling mathematical results of this century, known as Gödel's theorem, is that no axiomatic system for arithmetic can be both consistent and complete. In other words, when the sorting is all done (if such a thing were possible) there would always be statements about arithmetic that are left over. These statements cannot be proved either true or false. They are undecidable within that system. (See FIGURE 4).

What can we learn about life from these results about axiomatic systems? It seems clear to me that in life, we need to separate true statements from false ones. If we wish to take a rational approach to the sorting process, then we need to choose some sort of axiomatic system to live by. Here is a list of some of the lessons that I believe are applicable to any set of axioms for life:

1. There must be some undefined terms.
   Trying to define every term leads to circular definitions and confusion. Defining "God" in life is like defining "Point" in geometry. The real meaning comes not from attempts to define the term, but rather from the relationships contained in the axioms.

2. There must be axiomatic statements.
   In life, these are basic statements about undefined terms that cannot be proved true or false. These are the faith statements on which the system is built. The standard for acceptance or rejection of these statements cannot be proof. One tries to avoid inconsistency, but beyond that, any correspondence to reality is either good fortune or revelation.

3. There must be an existence axiom if we are to believe in existence at all.
   The alternative to rejecting existence altogether is to accept an existence axiom of some sort. In the latter case, the fundamental choice is between internal existence (e.g. I exist), and external existence (e.g. God exists).

4. Proving consistency is likely to be very difficult.
   Even if all we want to know about is arithmetic, belief in the consistency of our axiomatic system requires a leap of faith.

5. No axiomatic system can possibly allow us to prove all true statements.
   Not even in the area of arithmetic, which is the best known of all axiomatic systems, can we hope to find all truth.

6. Statements that can be proved only make explicit that which is already implicit in the axioms.
   Take, for example, the statement "God exists." If it can be shown to be true within a given axiomatic system, then it is either an axiom, or else it is implicit within the axioms. In the latter case, then there must be an existence axiom which is considered even more fundamental. On the other hand, if it can be shown to be false within an axiomatic system, then it is because the axioms preclude it, either explicitly or implicitly.

In view of these results about axiomatic systems, let us focus on the remarkable set of statements from Mosiah 2:13-17 quoted at the beginning of this paper. My comments are on the right.

I highly recommend these statements as axioms for life. I do not find them inconsistent. On the contrary, I find them full of potential for stimulating a meaningful life and an infinite horizon of learning of the things that God has created. Since the passage does not end at the ellipsis, let me conclude with the last phrase of the verse 17:

And now, if ye believe all these things, see that ye do them.